this post was submitted on 21 Sep 2024

1311 points (97.4% liked)

Science Memes

11205 readers

2290 users here now

Welcome to c/science_memes @ Mander.xyz!

A place for majestic STEMLORD peacocking, as well as memes about the realities of working in a lab.

Rules

Don't throw mud. Behave like an intellectual and remember the human.
Keep it rooted (on topic).
No spam.
Infographics welcome, get schooled.

This is a science community. We use the Dawkins definition of meme.

Research Committee

[email protected]

Other Mander Communities

Science and Research

Biology and Life Sciences

Physical Sciences

Humanities and Social Sciences

Practical and Applied Sciences

Memes

Miscellaneous

founded 2 years ago

MODERATORS

[email protected]

1311

Square! (lemmy.zip)

submitted 2 months ago by Maven to c/[email protected]

150 comments fedilink hide all child comments

you are viewing a single comment's thread
view the rest of the comments

[–] [email protected] 1 points 2 months ago* (last edited 2 months ago) (1 children)

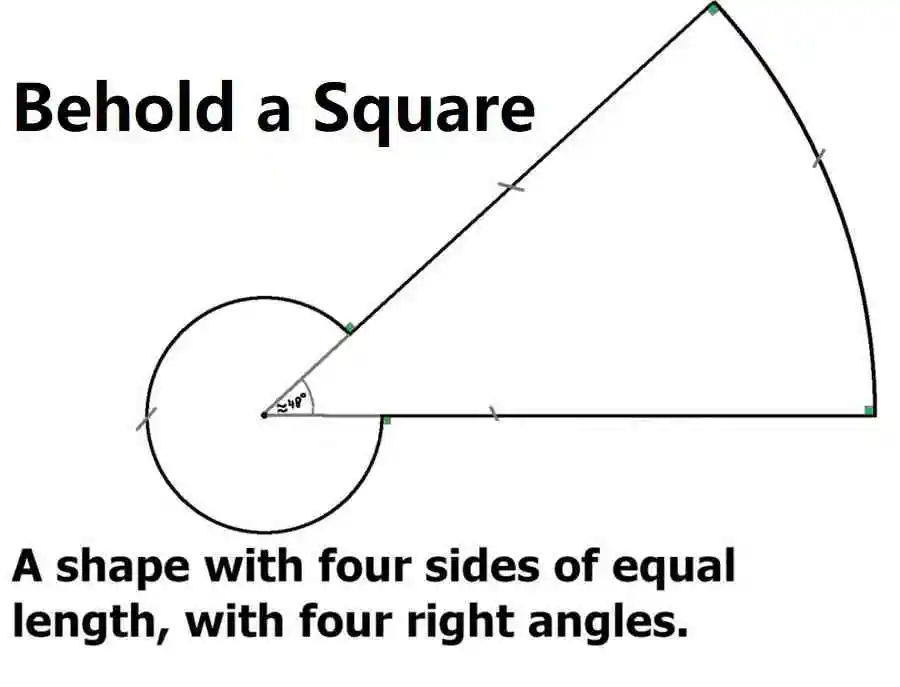
Sorry that’s not what I’m saying.

I’m saying a line with constant tangent would be a circle not a line.

Let me try another way, a function with constant first derivative in polar coordinates, would draw a circle in Cartesian

[–] [email protected] 1 points 2 months ago (1 children)

Given r=f(θ), we are generally not concerned with r′=f′(θ); that describes how fast r changes with respect to θ

I think this part from the textbook describes what you're talking about

Instead, we will use x=f(θ)cosθ, y=f(θ)sinθ to compute dydx.

And this would give you the actual tangent line, or at least the slope of that line.

[–] [email protected] 1 points 2 months ago* (last edited 2 months ago) (1 children)

But then your definition of a straight line produces two different shapes.

Starting with the same definition of straight for both. Y(x) such that y’(x) = C produces a function of cx+b.

This produces a line

However if we have the radius r as a function of a (sorry I’m on my phone and don’t have a Greek keyboard).

R(a) such that r’(a)=C produces ra +d

However that produces a circle, not a line.

So your definition of straight isn’t true in general.

[–] [email protected] 1 points 2 months ago (1 children)

I think we fundamentally don't agree on what "tangent" means. You can use

x=f(θ)cosθ, y=f(θ)sinθ to compute dydx

as taken from the textbook, giving you a tangent line in the terms used in polar coordinates. I think your line of reasoning would lead to r=1 in polar coordinates being a line, even though it's a circle with radius 1.

[–] [email protected] 0 points 2 months ago* (last edited 2 months ago) (1 children)

Except here you said here

https://lemmy.ml/comment/13839553

That they all must be equal.

Tangents all be equal to the point would be exponential I thinks. So I assume you mean they must all be equal.

Granted I assumed constant, because that’s what actually produces a “straight” line. If it’s not, then cos/sin also fall out as “straight line”.

So I’ve either stretched your definition of straight line to include a circle, or we’re stretching “straight line”

[–] [email protected] 1 points 2 months ago (1 children)

Given r=f(θ), we are generally not concerned with r′=f′(θ); that describes how fast r changes with respect to θ

You're using the derivative of a polar equation as the basis for what a tangent line is. But as the textbook explains, that doesn't give you a tangent line or describe the slope at that point. I never bothered defining what "tangent" means, but since this seems so important to you why don't you try coming up with a reasonable definition?

[–] [email protected] 0 points 2 months ago* (last edited 2 months ago)

My whole point is that a “straight done”, in general, doesn’t exist in the first place. Because in general definitions are actually really hard.

It’s not that it’s important to me. It’s that I’ve spent many parts of my day on the phone with the bank, and never should be taken for more than an asshole on the internet. Sorry if you thought I was more invested than that.