this post was submitted on 31 Oct 2024
184 points (97.4% liked)
memes
22780 readers
382 users here now
dank memes
Rules:
-
All posts must be memes and follow a general meme setup.
-
No unedited webcomics.
-
Someone saying something funny or cringe on twitter/tumblr/reddit/etc. is not a meme. Post that stuff in /c/slop
-
Va*sh posting is haram and will be removed.
-
Follow the code of conduct.
-
Tag OC at the end of your title and we'll probably pin it for a while if we see it.
-
Recent reposts might be removed.
-
No anti-natalism memes. See: Eco-fascism Primer
founded 4 years ago
MODERATORS
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
Think of the election as a Bus route from source, S, to Target, T. a directed graph G=(V,E), where V is the set of vertices (nodes) and E is the set of edges. Each edge (i,j)∈E has an associated non-negative cost (or length) c~ij~
Let x~ij~ be a binary variable that equals 1 if edge (i,j) is included in the shortest path, and 0 otherwise.
Minimize ∑_(i,j)∈E [c~ij~x~ij~]
Subject to:
∑_j:(s,j)∈E[x~sj~]−∑_i:(i,s)∈E [x~is~]=1
∑_i:(i,t)∈E [x~it~]−∑_j:(t,j)∈E [x~tj]~=−1
∑_i:(i,k)∈E [x~ik~]−∑_j:(k,j)∈E [x~kj~]=0∀k∈V∖{s,t}
x~ij~∈{0,1}∀(i,j)∈E
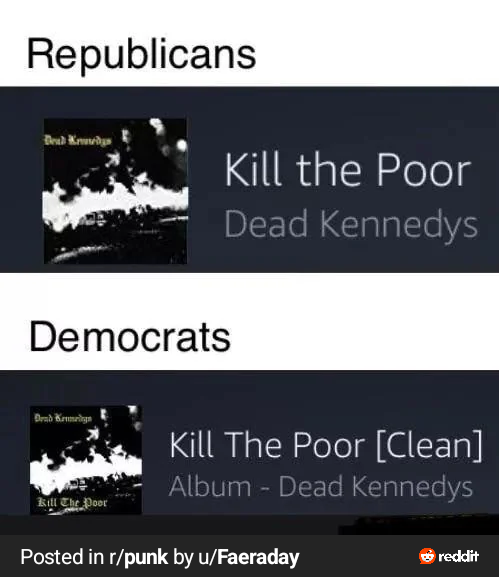
Thanks, that really cleared it up for me