this post was submitted on 31 Oct 2024
184 points (97.4% liked)
memes
22780 readers
354 users here now
dank memes
Rules:
-
All posts must be memes and follow a general meme setup.
-
No unedited webcomics.
-
Someone saying something funny or cringe on twitter/tumblr/reddit/etc. is not a meme. Post that stuff in /c/slop
-
Va*sh posting is haram and will be removed.
-
Follow the code of conduct.
-
Tag OC at the end of your title and we'll probably pin it for a while if we see it.
-
Recent reposts might be removed.
-
No anti-natalism memes. See: Eco-fascism Primer
founded 4 years ago
MODERATORS
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
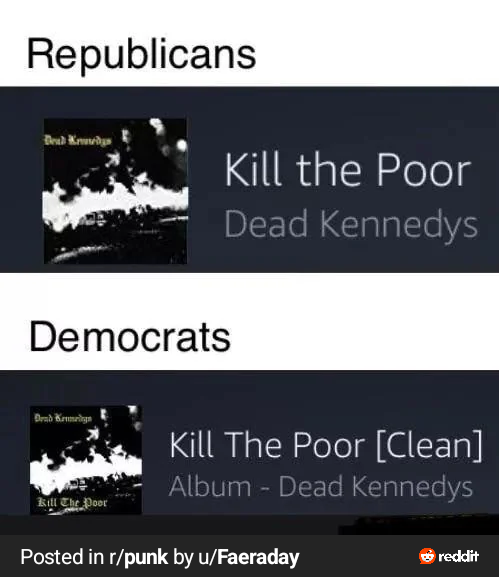
"Think of this election like a bus ride. You’ve got three busses: one takes you half way home, but you need to walk the rest of the way in the rain. The second takes you 75 miles in the wrong direction. The third never actually leaves the station. Which bus are you taking?
If you wanna argue that walking halfway home in the rain sucks, instead of acknowledging that the other two options are significantly worse then you’re the fucking problem. Shut the fuck up and get on the bus."
Think of the election as a Bus route from source, S, to Target, T. a directed graph G=(V,E), where V is the set of vertices (nodes) and E is the set of edges. Each edge (i,j)∈E has an associated non-negative cost (or length) c~ij~
Let x~ij~ be a binary variable that equals 1 if edge (i,j) is included in the shortest path, and 0 otherwise.
Minimize ∑_(i,j)∈E [c~ij~x~ij~]
Subject to:
∑_j:(s,j)∈E[x~sj~]−∑_i:(i,s)∈E [x~is~]=1
∑_i:(i,t)∈E [x~it~]−∑_j:(t,j)∈E [x~tj]~=−1
∑_i:(i,k)∈E [x~ik~]−∑_j:(k,j)∈E [x~kj~]=0∀k∈V∖{s,t}
x~ij~∈{0,1}∀(i,j)∈E