if 0.333... = 1/3 then 0.999... = 3/3 = 1
chapotraphouse
Banned? DM Wmill to appeal.
No anti-nautilism posts. See: Eco-fascism Primer
Vaush posts go in the_dunk_tank
Dunk posts in general go in the_dunk_tank, not here
Don't post low-hanging fruit here after it gets removed from the_dunk_tank
lots of good proofs in this thread but this one gets points for being by FAR the shortest while still being completely based on intuition and makes complete sense with an average high school mathematics background
and wants to know why 0.999... = 1
\begin{align} 0.999.... &= 9\cdot(0.1+0.01+0.001+... ) \ &= 9\cdot( 0.1^1 + 0.1^2 + 0.1^3 + ... ) \ &= 9\cdot(\sum\limits_{k=1}^\infty ( \frac{1}{10^k} ) ) \ &= 9\cdot(\sum\limits_{k=0}^\infty ( \frac{1}{10^{(k+1)}}))\ &= 9\cdot(\sum\limits_{k=0}^\infty \frac{1}{10}*(\frac{1}{10^k})) \ &= \frac{9}{10}\cdot (\sum\limits_{k=0}^\infty (\frac{1}{10^k})) \ &= \frac{9}{10}\cdot \frac{1}{(1-(\frac{1}{10}))}\ &= \frac{9}{10}\cdot \frac{10}{9} = 1 \end{align}
The crux rests on a handy result on from calculus: the sum of an infinite geometric series looks likes s = 1/(1-r), when s = \sum\limits_k=0^inf r^k, and |r| < 1.
Sorry for the latex. When will hexbear render latex? This is a bit more readable:
(aesthetic edit for our big beautiful complex analysts)
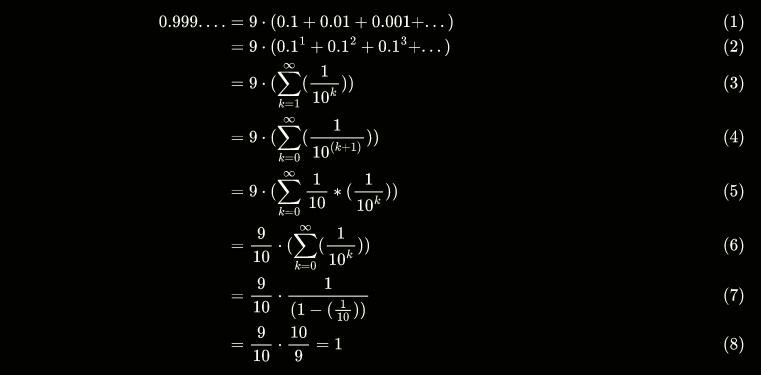
Never thought of employing the geometric series for this, that’s clever.
^_^ thank you!
Using i as an index 🤮
? Thats pretty standard though right?
in computer programs, yes
not so much in analysis
I'm seeing n and i used as variables in Rudin, predominantly n though, but Im accustomed to n being a constant.
The symbol 'i' is usually reserved for the imaginary unit.
I've seen it used very frequently as a name for a variable, the imaginary unit i usually has a different typeface to distinguish the two is what Im accustomed to.
Your feedback is valid and I apologize for rendering such an ugly proof
The thing that really got 0.999...=1 to click on my mind is the fact that you can't find a number between 0.999... and 1. You might think "Just put something at the end of 0.999...," but there is no end to 0.999....
Yay, Dedekind cuts are finally useful!
so, start with:
x = 0.999...
now multiply each side by 10
10x = 9.9999....
now we subtract x from the left side, and 0.999... from the right, which is fine because they are equal:
9x = 9
and from there it should be fairly obvious that x is also equal to 1, which means 0.999... is also equal to 1
0.999..=1 because it's funny that people get so mad about it
I agree, but the little guy does need rigour, or he will starve under crapitalism.
I didn't have any bread to bring him but I had plenty of roses
He's hungry

Feed him
I suppose I will post one myself, as I do not expect anybody else to have that one in mind.
The decimals '0.999...' and '1' refer to the real numbers that are equivalence classes of Cauchy sequences of rational numbers (0.9, 0.99, 0.999,...) and (1, 1, 1,...) with respect to the relation R: (aRb) <=> (lim(a_n-b_n) as n->inf, where a_n and b_n are the nth elements of sequences a and b, respectively).
For a = (1, 1, 1,...) and b = (0.9, 0.99, 0.999,...) we have lim(a_n-b_n) as n->inf = lim(1-sum(9/10^k) for k from 1 to n) as n->inf = lim(1/10^n) as n->inf = 0. That means that (1, 1, 1,...)R(0.9, 0.99, 0.999,...), i.e. that these sequences belong to the same equivalence class of Cauchy sequences of rational numbers with respect to R. In other words, the decimals '0.999...' and '1' refer to the same real number. QED.
I like how compact this one is ;)
Had a little trouble following this as plain text, so I wrote it up in LaTeX (it'll be a bit small if you try to read it inline--you'll probably want to tap to enlarge on mobile or open the image in a new tab/click this direct link to the image):

I tried to hew as closely to your notation as I could, but let me know if you spot any errors!
Thank you.
And no, I do not notice any errors.
I should re-learn Lateχ.
I will be posting another another proof, one using the assumption that 0.999... is the sum of the series 9/10+9/100+9/1000+... (and that 1 is the sum of the series 1+0+0+0+...), unless somebody else comes here and feeds it to the little guy first.
(I haven't done real math since forever)
Part 1: Proving If x,y are distinct positive real numbers and x < y, there is a z in R such that x < z < y.
Let y = x + e, where e is in R. e is also positive because:
x < y
x < x + e
0 < e
x < z < y becomes x < z < x + e. We can then choose z = x + 0.5e so that
x < z < y
x < x + 0.5e < x + e
0 < 0.5e < e
0.5e - 0.5e < 0.5e + 0 < 0.5e + 0.5e
-0.5e < 0 < 0.5e
Since we've shown earlier that e > 0, -0.5e < 0 < 0.5e is true no matter what e.
Part 2: Decimal Notation
Decimal notation is written as the sequence a~m~a~m-1~...a~1~a~0~.b~1~b~2~...b~n~, where a,b are in the set {0,1,2,3,4,5,6,7,8,9}. The sequence a~m~a~m-1~...a~1~a~0~.b~1~b~2~...b~n~ itself is of the number a~m~10^m^ + a~m-1~10^m-1^ + ... + a~0~10^0^ + b~1~10^-1^ + b~2~10^-2^ + ... + b~n~10^-n^.
Part 3: The actual proof through proof by contradiction
Let x = 0.999... and y = 1. This means there exists a z that is between 0.999... and 1. So let's construct z = a~0~.b~1~b~2~...b~n~. a~0~ has to be either a 0 or 1 and since there is no number smaller than 1 with 1 as its first digit, a~0~=0. z = 0.b~1~b~2~...b~n~
0.999... = 9*10^-1^ + 9*10^-2^ + 9*10^-3^ + ... while z = b~1~10^-1^ + b~2~10^-2^ + ... + b~n~10^-n^. If 0.999... < z, then
0.999... - z < 0
9*10^-1^ + 9*10^-2^ + 9*10^-3^ + ... - (b~1~10^-1^ + b~2~10^-2^ + ... + b~n~10^-n^) < 0
(9*10^-1^ - b~1~10^-1^) + (9*10^-2^ - b~2~10^-2^) + (9*10^-3^ - b~3~10^-3^) + ... < 0
(9 - b~1~)*10^-1^ + (9 - b~2~)*10^-2^ + (9 - b~3~)*10^-3^ + ... < 0
But as we've established in Part 2, b~1~, b~2~, b~3~, etc have to be from the set {0,1,2,3,4,5,6,7,8,9}, meaning (9 - b~n~) > 0 for any n. Therefore, (9 - b~1~)*10^-1^ + (9 - b~2~)*10^-2^ + (9 - b~3~)*10^-3^ + ... cannot be less than 0.
The theorem requires for x and y to be distinct positive real numbers and x < y, and since 0.999... and 1 can be trivially shown to be positive real numbers, this means that 0.999... and 1 are not distinct. In other words, 0.999... = 1.
Alright, so, the other proof that I promised:
If we define 0.999... as the sum of the series 9/10+9/100+9/1000+..., then for every neighbourhood U(1) it is true that there exists a metric ball B_N = B(1, 1/10^N), where N is natural, such that B_N is a subset of U(1).
For all natural n > N it is true that d(sum(9/10^k) for k from 1 to n, 1) = |1 - sum(9/10^k) for k from 1 to n| = |1/10^n| = 1/10^n < 1/10^N, meaning that for all natural n > N it is true that sum(9/10^k) for k from 1 to n is in B_N, meaning that it is also in U(1).
However, sum(9/10^k) for k from 1 to n is the nth partial sum of the series 9/10+9/100+9/1000+..., which, together with the fact that every such sum is in U(1) for n > N, means that 1 is the limit of the sequence of the partial sums of the series 9/10+9/100+9/1000+..., meaning that 1 is the sum of that series. That means that 0.999... is 1 by definition.
The ellipses mean infinity. Anything less than infinity and the equation is false. It looks unintuitive because infinity is unintuitive
The ellipses mean infinity
No, it does not. The ellipsis notation is used to denote a repeating pattern. It is not used to denote points that are named 'infinity' in spaces like Aleksandrov compactification and the extended space of real numbers.
I am sorry, but your reply lacks rigour.
Is this a bit? I meant that the ellipses, in this context, mean that the nines go on forever. Obviously there are other symbols used to represent similar ideas, like ∞
I'm being serious. The word 'infinity' refers to some points from spaces like Aleksandrov compactification. It does not refer to any sort of repetition of any pattern. You cannot, for example, write '0.999∞' or '0.999infinity' to mean the same thing as '0.999...' or '0.(9)'.
ok mothematician
